Consistent Hashing with Clojure
In this post, I have tried explaining what Consistent Hashing is, when it is needed and how to implement it in Clojure. Consistent hashing has many use cases. I have chosen the use case of distributed caching for this post.
Caching
Almost all applications today use some kind of caching. Caches help reduce the number of requests served by your database and improve latency. Initially, your application would have one cache node sitting over your database. On read paths, it will be checked if data is available on the cache node, if not, you would go to the database and populate the data on your cache node. On write paths, you would first update the database and then your cache. Or let the cached item expire with some TTL according to your consistency requirements. With this setup, you are using your cache node as a superfast index to look up hot items and absorb traffic that would have otherwise gone to your database.
But as your application usage grows, your cache node is also going to get overwhelmed and soon enough, you will need multiple cache nodes. When you have multiple nodes, you will need to decide how you are going to divide data between those nodes.
Distributed Caching
One very simple strategy to divide data between cache nodes is to take an integer hash of the cache key and then take the mod by the number of cache nodes.
For example, if the hash of the cache key came out to be 86696499 and if we have
4 servers, then (86696499 mod 4) = 3; so the data should be in the node with
index 3 (0 based indexes).
This is very simple to implement. For simplicity, we will use email addresses of users as cache keys.
(require '[clojure.pprint :as pp])
(def emails ["Bob@example.com" "Carry@example.com" "Daisy@example.com"
"George@example.com" "Heidi@example.com" "Mark@example.com"
"Steve@example.com" "Zack@example.com"])
(defn get-node
"Returns which node shall be used for the given `object` when `n`
cache nodes are there."
[n object]
(-> object hash (mod n)))
(defn get-distribution
"Returns distribution of `objects` over `n` nodes."
[n objects]
(reduce (fn [acc object]
(let [node (get-node n object)]
(update acc
(str "node-" node)
(fnil conj [])
object)))
{}
objects))
;; For printing maps in sorted order of keys
(->> emails (get-distribution 4) (into (sorted-map)) pp/pprint)Let’s go through the code above.
emails is just a collection of emails.
get-node tells us which object should go on which node. This was the logic
that we discussed previously. We are first taking a hash and then taking mod n
of that hash.
get-distribution just runs get-node on emails and returns a map which has
node names as keys and corresponding values as list of keys which would reside
on those nodes.
The last line prints how emails will be divided on cache nodes if we had 4
cache nodes. It prints the following map:
{"node-0" ["Bob@example.com" "Steve@example.com" "Zack@example.com"],
"node-1" ["Carry@example.com" "Daisy@example.com" "George@example.com"],
"node-2" ["Mark@example.com"],
"node-3" ["Heidi@example.com"]}Okay so this seems to be working well! Now every time we have to fetch some data, we will just check on which node that data is expected and then we will try to fetch it from that node. So far so good!
So why do we need consistent hashing if mod n hashing is working well?
In today’s distributed infrastructure, the total number of cache nodes can easily change. There could be multiple reasons such as, needing a few extra nodes when more traffic is expected, or a node going down due to some error.
We can simulate the above 2 situations.
Let’s say we add another cache node in our cluster. We can simulate this by running:
(->> emails (get-distribution 5) (into (sorted-map)) pp/pprint)We will get the following:
{"node-0" ["Bob@example.com"],
"node-1" ["Daisy@example.com"],
"node-2" ["Steve@example.com"],
"node-3" ["Carry@example.com" "George@example.com" "Mark@example.com"],
"node-4" ["Heidi@example.com" "Zack@example.com"]}If we compare the distribution of keys for 4 nodes vs 5 nodes, we can see that literally 6 out of 8 keys have different nodes now.
The same will happen if a node goes down. Let’s simulate this by running:
(->> emails (get-distribution 3) (into (sorted-map)) pp/pprint)This produces:
{"node-0" ["Zack@example.com"],
"node-1" ["Bob@example.com" "Daisy@example.com" "George@example.com"],
"node-2" ["Carry@example.com" "Heidi@example.com" "Mark@example.com" "Steve@example.com"]}In this case as well, 5 out of 8 keys now have a different node.
Both of these cases create a really bad situation for our databases. Our data is going to be residing on 4 nodes initially. Once we add or remove nodes, almost all of the keys are going to get relocated. This is going to result in a flurry of cache misses and all the missed requests will go to our databases, creating a hotspot.
This is clearly undesirable and in extreme situations, this could even take our entire system down.
Let’s understand why this is happening. We need to remember that our logic to
select nodes (get-node) for data includes number of nodes as a parameter. So
when our number of nodes changes, clearly the output of get-node is most
likely to change.
We need to find a strategy which will not directly depend on the number of nodes that we have.
Consistent Hashing
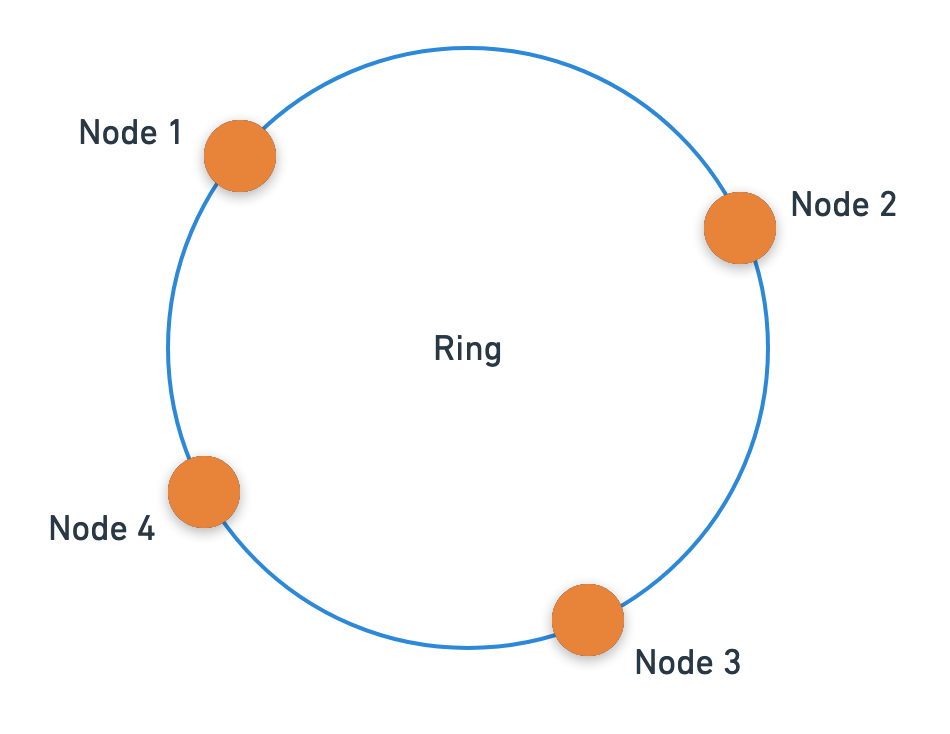
Consistent hashing is a simple method of hashing which does not depend on the number of nodes we have. In consistent hashing, we imagine our nodes to be placed on a ring. The ring is made up of the range of our hash function. For example, if our hash function produced hashes over the entire range of integers, then the ring would go from the minimum integer to the maximum integer.
We will generate hashes for nodes using some unique property of nodes, say IP addresses. These hashes will be the locations of our nodes on the ring.
To insert or retrieve data, we will hash the caching key and use the node which is closest to the caching key hash in the clockwise direction. (Clockwise is just a convention we are using for this post. Anti-clockwise will also work.)
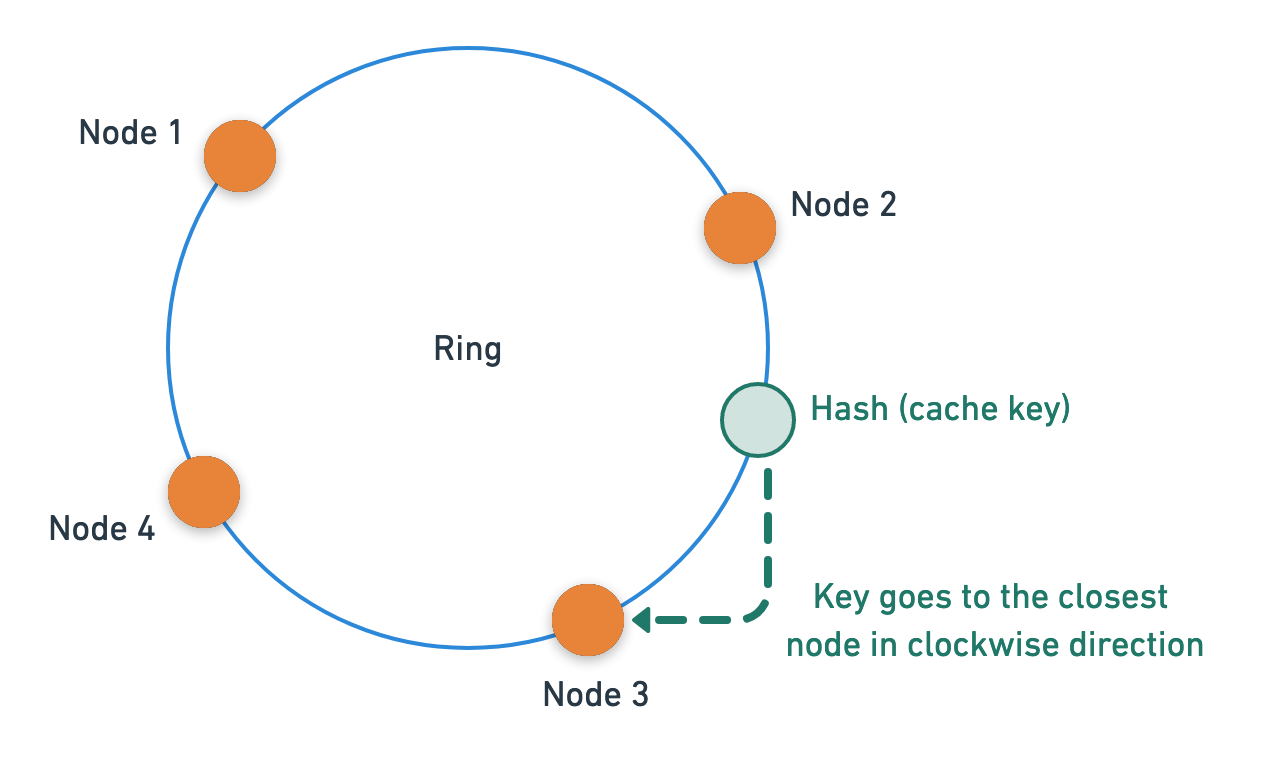
What benefit has this given us?
Well, so far it does not look like this is useful. In fact, we are doing more work to find out which data goes to which node. We will now consider the 2 cases that we discussed for mod n hashing.
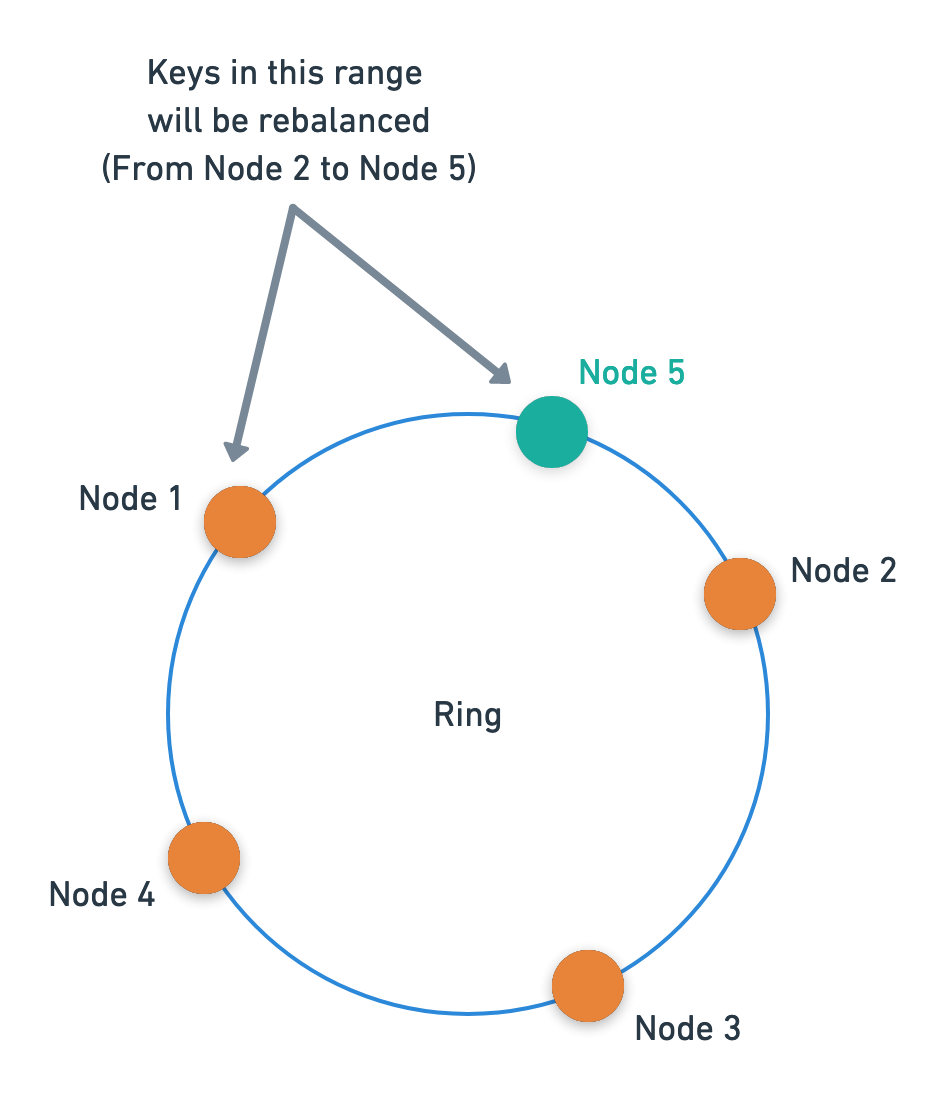
Let’s say we add a 5th node to our ring.
If the 5th node got placed between the 1st and the 2nd node, think about which keys will get relocated. Only the keys between 1st and 5th node will be relocated to the 5th node. All the keys on the rest of the ring will remain where they were.
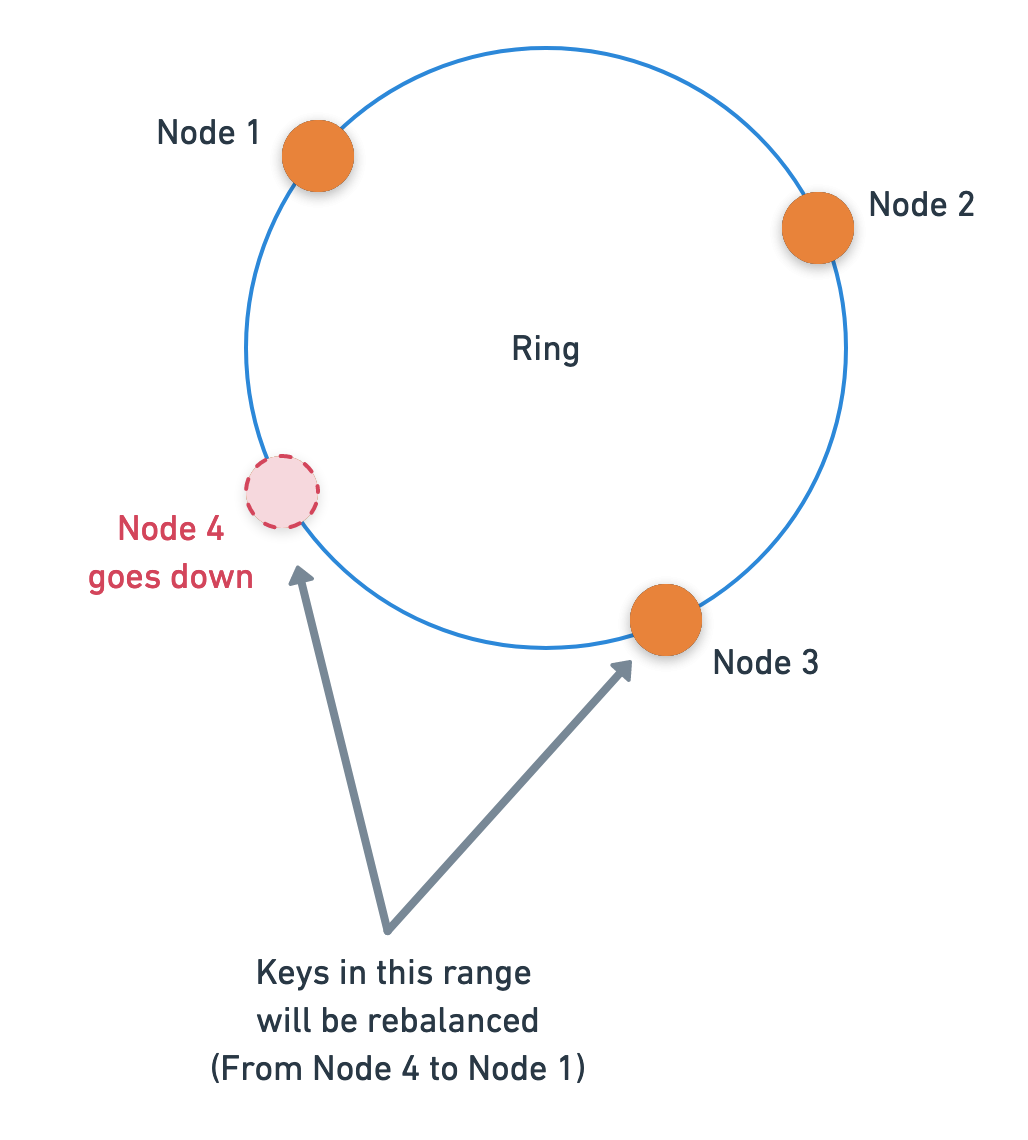
Similarly, if one of our nodes, say the 4th node, goes down; then only the keys between the 3rd and 4th will get relocated.
When nodes are added or removed, only count(keys) / count(nodes) number of
keys will be relocated. This will reduce the number of cache misses by a huge
amount and save our databases from hotspots!
(There is a small caveat here which is discussed later.)
Implementation in Clojure
We will write a simple API for consistent hashing. This will include functions
to manage the ring: create-ring, add-node, remove-node. And like before,
we will have a get-node function.
Let’s look at create-ring first.
(defn create-ring
"Creates a ring for `nodes`.
`nodes` should be a coll of property of nodes which should be used
for placing the nodes on the ring.
Returns a ring data structure. It is a map which looks like this:
{:node-hashes <a list containing hashes of `nodes` (order is preserved) >
:hash->node <a map which is a look up table which gives node descriptor
given a hash to a hash> }
The return value of this function should be preserved by the caller as it is
required as input to other functions in this API.
"
[nodes]
(let [nodes (set nodes)
node-hashes (->> nodes
(map hash)
sort)
hash->node (reduce (fn [acc node]
(assoc acc
(hash node)
node))
{}
nodes)]
{:node-hashes node-hashes
:hash->node hash->node}))We are taking the set of nodes to make sure there are no duplicate
entries. Then we get the hash values for all the nodes and sort them in
ascending order. This sorted list will be used to find the closest node in the
ring. We also create a lookup table hash->node which gives us the node
corresponding to a given hash. Finally, we return both of these so that they can
be passed to other functions in our API.
Let’s see how add-node and remove-node work.
(defn add-node
"Adds `node` to existing `ring`.
`ring` is expected to be a ring data structure (see doc string of
`create-ring`.)
`node` is expected to be a node descriptor (see doc string of `create-ring`).
Returns a ring data structure (see doc string of `create-ring`).
"
[ring node]
(let [current-nodes (-> ring :hash->node vals)]
(-> current-nodes
(conj node)
create-ring)))
(defn remove-node
"Removes `node` from existing `ring`.
`ring` is expected to be a ring data structure (see doc string of
`create-ring`.)
`node` is expected to be a node descriptor (see doc string of `create-ring`).
Returns a ring data structure (see doc string of `create-ring`).
"
[ring node]
(let [current-nodes (-> ring :hash->node vals)]
(->> current-nodes
(remove #(= % node))
create-ring)))As you can see, these are very simple functions which just get current-nodes from the
ring and then add or remove a node and call create-ring again. This works
because our hash function is repeatable. So creating the ring again generates the same
hash values for existing nodes.
Let’s look at the last function in our API, get-node.
(defn get-node
"Returns node to be used for cache-key `k`."
[ring k]
(let [node-hashes (:node-hashes ring)
key-hash (hash k)
closest-hash (or (->> node-hashes
(drop-while #(< % key-hash))
first)
(first node-hashes))]
(get (:hash->node ring) closest-hash)))The main logic in this function is to find the closest node to the cache-key, in clockwise direction.
(or (->> node-hashes
(drop-while #(< % key-hash))
first)
(first node-hashes))node-hashes is the sorted list of hashes of our nodes. We are dropping the
nodes which have hashes lesser than the hash of the cache-key. We will stop
dropping once we find a value greater than key-hash. This value will be the
hash of the closest node in clockwise direction. If key-hash is greater then
all the values in node-hashes, we wrap around and select (first
node-hashes). For simplicity, I have used sequential search for finding the
closest hash. Binary search could be used for making this more effecient.
Now our API for consistent hashing is complete and ready for use!
Let’s use it for the same example scenarios that we used for mod n hashing.
(require '[clojure.pprint :as pp])
(def emails ["Bob@example.com" "Carry@example.com" "Daisy@example.com"
"George@example.com" "Heidi@example.com" "Mark@example.com"
"Steve@example.com" "Zack@example.com"])
(def nodes ["node-0" "node-1" "node-2" "node-3"])
(defn get-distribution
[nodes objects]
(let [ring (create-ring nodes)]
(reduce (fn [acc object]
(let [node (get-node ring object)]
(update acc
node
(fnil conj [])
object)))
{}
objects)))
;; For printing maps in sorted order of keys
(->> emails (get-distribution nodes) (into (sorted-map)) pp/pprint)Result with 4 nodes:
{"node-0" ["Daisy@example.com" "George@example.com"],
"node-1" ["Mark@example.com" "Zack@example.com"],
"node-2" ["Bob@example.com" "Heidi@example.com"],
"node-3" ["Carry@example.com" "Steve@example.com"]}With a node added:
(->> emails (get-distribution (conj nodes "node-4")) (into (sorted-map)) pp/pprint)
{"node-0" ["Daisy@example.com" "George@example.com"],
"node-1" ["Mark@example.com" "Zack@example.com"],
"node-2" ["Heidi@example.com"],
"node-3" ["Carry@example.com" "Steve@example.com"],
"node-4" ["Bob@example.com"]}Only 1 out of 8 keys got relocated!
With node-3 removed:
(->> emails (get-distribution (drop-last nodes)) (into (sorted-map)) pp/pprint)
{"node-0" ["Daisy@example.com" "George@example.com"],
"node-1" ["Mark@example.com" "Zack@example.com"],
"node-2" ["Bob@example.com" "Carry@example.com" "Heidi@example.com" "Steve@example.com"]}Only 2 out of 8 keys got relocated. We can see that node-3 keys are now with
node-2. Keys with node-0 and node-1 have not changed at all.
Caveats
Our implementation above is not something that can be used in production. The problem is that when we have only a few nodes, we could land up in a situation like this:
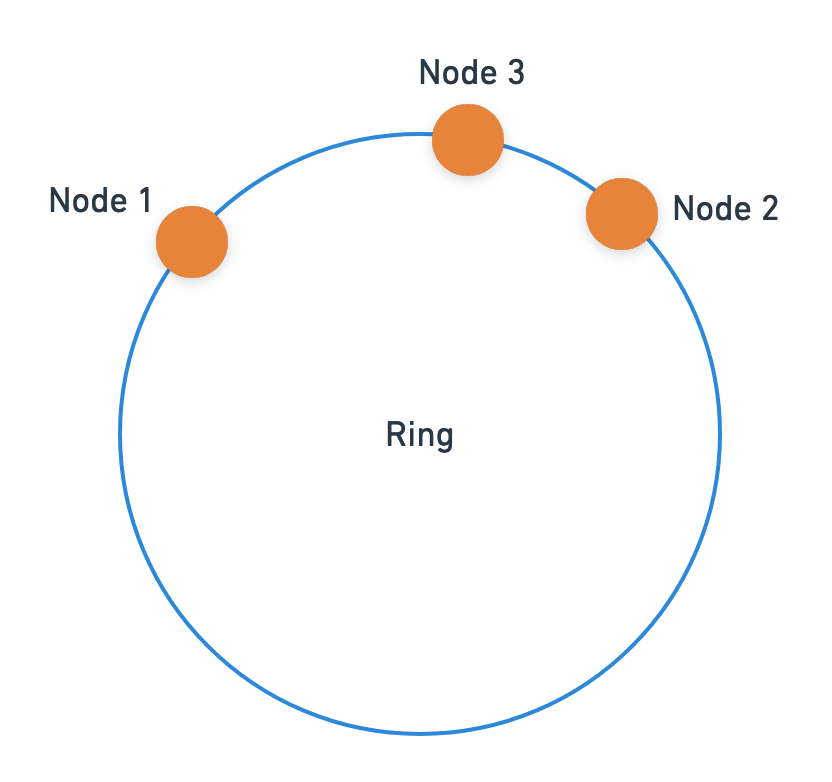
In the above situation, most of the keys will go to Node 1.
The solution is simple. Instead of having just one hash per node, we could have multiple hashes which map to the same node. This will ensure more randomness and a better distribution of keys. It will look like this:
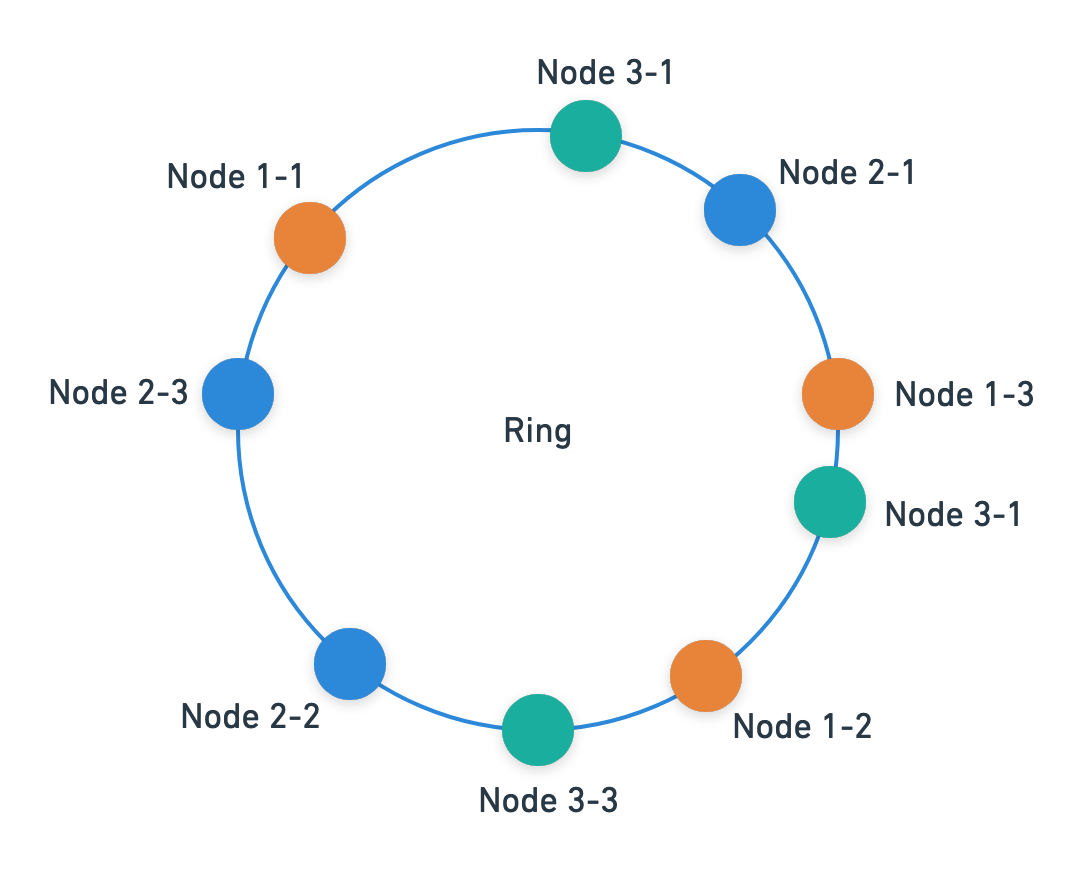
Conclusion
-
Consistent hashing is a simple and great caching strategy to make sure your databases are protected from hotspot in a distributed environment.
-
Consistent hashing is able to achieve this by getting rid of
number of nodesas a parameter to hashing. -
When nodes are added or removed, only
count(keys) / count(nodes)number of keys will be relocated. -
Many in-memory datastores today use consistent hashing.